

Hydrostatic pressure
Hydrostatic pressure plays a major role in all applications and activities that take place in liquids. This includes, among other things, pressure measurement in the industrial sector. With us, you will learn how hydrostatic pressure is defined, how it works and what effects its behavior has on measurement. Learn more!
How to define hydrostatic pressure?
The pressure in a fluid at rest (non-fluid), on which a homogeneous gravitational field acts, is called hydrostatic pressure. The higher the liquid column, the higher the pressure at the bottom of the tank. Thus, the hydrostatic pressure in a liquid increases with depth.
Similarly, the pressure depends on the density of the liquid. A liquid with a high density, such as water, exerts more pressure on the bottom than a liquid with the same volume but lower density, such as oil.
The external pressure also affects the pressure of the test liquid. For example, atmospheric pressure corresponds to the pressure exerted on the earth's surface by the weight of a column of air whose height is equal to the thickness of the earth's atmosphere. The average value of atmospheric pressure at sea level is 1013.25 hPa.
In open tanks, the liquid pressure is the sum of the pressure due to weight at a certain height and the atmospheric pressure above the level. In closed tanks, the external pressure is equal to the pressure above the surface of the liquid.
What factors influence hydrostatic pressure?
As mentioned above, the physical quantities that affect the hydrostatic pressure ph:
- is the gravitational acceleration constant g [m/s²],
- is the height of the liquid column h [m],
- the density of the liquid to be tested ρ [kg/m³] and
- the external pressure p0 [Pa].
What is the formula underlying hydrostatic pressure?
In the previous section, all physical quantities that influence the hydrostatic pressure of a liquid on the bottom of a vessel were listed. This results in the following formula for the hydrostatic pressure:
ph = ρ × g× h
What is the unit of hydrostatic pressure?
The unit of pressure is Pascal [Pa], the basic SI unit of pressure. It is defined as the pressure of gravity F of 1N on a surface of 1 m2. Here, the value of 1N corresponds to the force defined as the unit of mass of 1 kilogram multiplied by the acceleration due to gravity g = 10m/s2.
What is hydrostatic pressure? - A case study
Consider the pressure at the bottom of an open container of water at 4 °C. The density of the liquid is ρ = 1000 kg/m3. The height h of the water in the tank is 15 m. Assuming an atmospheric pressure of 1013.25 hPa and acceleration due to gravity g = 9.81 m/s2, the pressure of the liquid at the bottom of the tank is:
ph = 1000 kg/m3 × 9.81m/s2 × 15m + 1013.25hPa
ph = 1481,6hPa + 1013,25hPa =2494,85hPa = 2,49 bar
The actual value of the pressure at the bottom of the tank under consideration is 2.49 bar, and half of this value consists of the external pressure. Based on this result, it is not possible to calculate the height of the liquid column, since the result is the sum of hydrostatic pressure and variable atmospheric pressure. Therefore, pressure transmitters convert the difference between the pressure measurements at the bottom of the tank and above the surface of the liquid. In this way, the influence of the external pressure is compensated.
Practical Tip:
One meter of water column generates a hydrostatic pressure of approx.
0.1 bar.
What is the hydrostatic paradox?
The formula and the calculations above make it clear that it is not necessary to know the total volume of the vessel to calculate the pressure value. The necessary information is the density of the liquid as an independent property of the tested medium and the height of the liquid column. This results in a certain property called the hydrostatic paradox. Thus, the hydrostatic paradox describes a phenomenon in which the pressure at the bottom of a vessel filled with liquid does not depend on the shape of the vessel and the volume of the liquid. The pressure of the water column is always the same.
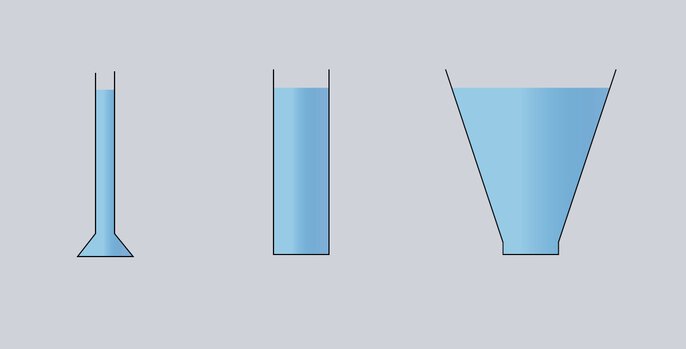
The hydrostatic pressure is the same for an identical fill level in all containers. The force acting on the bottom is also identical for the same bottom area.
What must be considered when installing a sensor?
The installation position of the sensor diaphragm is irrelevant for hydrostatic measurement. The pressure acts in all directions at any altitude. A pressure transmitter can be mounted on the side of the tank or suspended in the tank as a level probe. Only the mounting height is decisive for the measurement result - the measurement takes place from a complete covering of the diaphragm.

Bild 2: Hydrostatische Sonde für die Füllstandmessung JUMO MAERA S25
- ${title}${badge}


